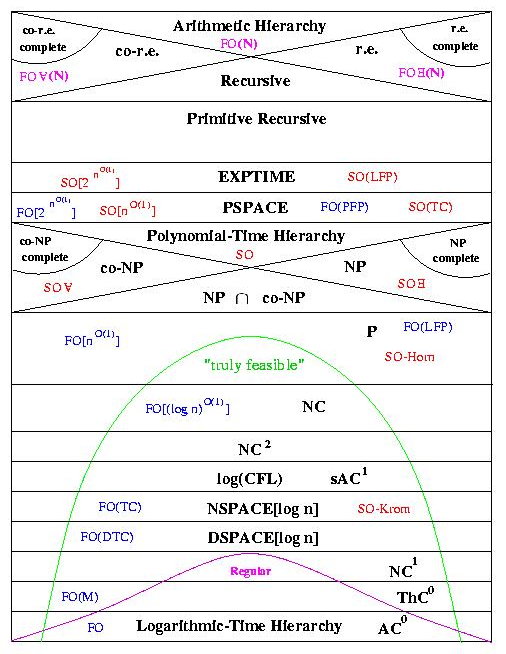
图灵等人的工作划定了可计算与不可计算问题的界限。不可判定问题构成上层结构，它们虽然都不可解，但存在难度差异。可判定问题构成下层结构，属于计算复杂性研究范畴，这些问题虽然理论上可解，但可能需要极长的计算时间（如指数时间）。问题的难度从最底层的AC⁰类开始（包含例如固定位数的加法运算问题）；往上是NC¹类、NC²类问题等等，这些问题在图灵机上相对简单；继续往上达到P类问题，是多项式时间内可解的问题；P类之上是NP类问题、PSPACE、EXPTIME等问题。计算复杂性领域的学者们通常认为这些类之间是真包含关系，但自上世纪70年代末提出计算复杂性理论以来，大量复杂性类之间的真包含关系尚未得到证明。

其中，要得到AC⁰和NC¹之间的真包含关系，需要证明某些布尔函数用合取范式表示困难，但用命题逻辑公式表示容易。即要证明某个问题对NC¹是容易的，对AC⁰是难的。（AC⁰是一个很小的计算模型，只计算固定深度的合取范式或析取范式，NC¹类问题对应所有可行的用多项式长的命题逻辑公式计算的问题。）直到上世纪80年代，姚奇志等学者观察到存在一个函数用AC⁰不能算，但显然能够用命题逻辑公式去算，这就是PAR问题（奇偶校验：判定一个01字符串中1的个数是否是奇数个）。在图灵机上该问题可以通过线性时间解决，只需从头到尾遍历并计数即可，但在其他模型上，如AC⁰上，该问题则较难解决。研究人员在80年代初成功证明相关结果，从而解决了第一个真包含问题，并引发了后续研究。

当时研究人员对此非常乐观，认为可以一路证明至P不等于NP。然而，寻找一个显式的、被证明不属于NC¹的问题仍然是一个开放性问题，这受到“自然证明障碍”的限制，也与密码学安全性密切相关。

具体来说，研究人员希望找到一个布尔函数，使得用命题逻辑公式表示时需要非常多的联结词，即公式必须非常长。然而要找到一个使得需要用指数多的联结词来描述的布尔函数，这在理论上非常困难。1942年香农在研究逻辑电路的过程中发现n元布尔函数的数量是，而命题逻辑公式能表示的函数数量远远少于所有布尔函数的数量，这意味着在布尔函数宇宙中绝大多数的函数都是难的，然而至今人们无法显式地指出其中一个并证明是难的。后来，苏联学者Razborov在1994年提出了一种方法论上的限制，称为“自然证明”。他指出，现有的证明方法使用的分离函数f的性质非常自然（如证明AC⁰不等于NC¹时选择的奇偶性问题可以用一句话描述）。这些函数的性质容易定义和验证，但无法用于证明不属于NC¹的问题，否则将能够破解现有的密码系统。密码系统使用的伪随机布尔函数或单向函数的输出看起来是随机的，没有规律，NC¹中存在很多这样的命题逻辑公式，如果用容易定义的f去证明，将能够压缩这些函数的真值表，从而快速列出其输出，这与密码系统的安全性产生矛盾。因此，自然证明的限制使得用容易定义的f无法证明P不等于NP，而不易定义的f又难以具体描述。这一结果导致90年代中后期许多研究人员转向其他方向，关于NC¹等复杂类的研究陷入停滞。

接下来，沈老师介绍自己围绕NC¹所做的工作。2024年其研究团队在ACM上发表了关于NC¹问题的最新研究成果，即奇偶性判定及其补问题对于一类非单调命题逻辑家族（包括回答集语义下的逻辑程序（Logic Program））是难解问题。

逻辑程序是非单调命题，与布尔公式表达力等价，任何布尔函数都可以用逻辑程序表示。LP是可以用小的逻辑程序容易计算的问题，NC¹是用小的布尔公式容易计算的问题，因此LP与NC¹两者之间存在密切联系，主要区别在于LP是非单调逻辑，而NC¹是单调逻辑。Razborov（2006）基于的假设，证明了存在一个P-完全问题PathPro对逻辑程序是容易的但对命题公式是难的问题。沈老师则进行反向思考，是否存在对逻辑程序困难但对NC¹容易的问题。突破点依然是PAR问题。沈老师研究证明PAR问题对于逻辑程序来说是难问题，且该证明无需基于有关复杂度之间关系的假设。计算输入长度为n的奇偶性问题的逻辑程序的长度s将满足：（在程序有loops的情况下，）。不仅如此，这一结果表明，在P类中还存在与AC-NC层次具有正交关系、互不包含的复杂性类，即基于非单调命题逻辑形式定义的复杂性类。这一发现为与AC-NC分层关联的计算复杂性研究提供了新的视角。

沈老师的研究结果进一步指出，、、问题对逻辑程序来说也是难问题。（是PAR的补问题，是判断一个字符串中1的个数是否是q的倍数。）

接着，沈老师继续分享了自己的证明思路，即如何通过应用布尔电路复杂性中的概率方法得到上述结果。证明的基本思路是要把逻辑程序转化为等价的命题公式，转换后的程序分为两部分：Completion Circuit部分保持原有规模，可将其中的规则直接视为命题逻辑的蕴涵式；另一部分Loop Circuit则产生指数级增长的公式，专门描述推理中的复杂循环依赖关系。没有循环依赖的程序可以直接转换为小规模的completion，并且能够由AC⁰线路处理。对于含有循环依赖的程序，则用概率方法（Hit & Collapse）来处理其中产生的极其复杂的相互依赖关系。沈老师以消消乐游戏来形象地类比Hit & Collapse方法。简单来说，这种方法使用随机限制（random restriction）来简化电路，当部分输入被固定为0或1，其他输入保持未定状态，一旦有合适的随机限制ρ作为输入，部分门（gate）就会被消除，电路深度随之缩减，这类似于消消乐游戏中的消除过程。析取和合取运算就具有这样的特质——少量输入变化就能显著影响输出。析取操作只要有一个输入为1输出就为1，合取操作只要有一个输入为0输出就为0。Håstad（1986）证明了对于所有AC⁰线路存在某种限制方式可以在未读取全部输入时就产生输出，这与奇偶性判断必须考虑所有输入的特性形成矛盾。这种矛盾揭示了AC⁰线路无法有效解决奇偶性问题的本质原因。

然而接下来面临的问题是，Håstad的方法只适用于多项式大小的深度固定的电路，面对很大的深度固定的电路时，需要寻找另外合适的Hit。受香农推导论证的启发，沈老师通过概率算法证明了合取门输入超过100个时也是容易消除的。具体理论如下图：

此外，沈老师给出判定对逻辑程序是“难问题”的充分条件，定义了“Robustness”概念：判定函数输出所需读取的最小输入位数。对于不同逻辑运算，所需最小位数差异显著，例如，合取/析取运算最少需查看1位，PAR_n运算则需要读完n位。沈老师的研究证明，若函数f需要读取超过位才能判定输出，则对逻辑程序而言该函数是难问题。这种判定问题难度的方法可以通过这样的直观来理解：面对一道习题，简单题目也许不用读完就能知道答案，而难题或许需要读很多遍才能理解。

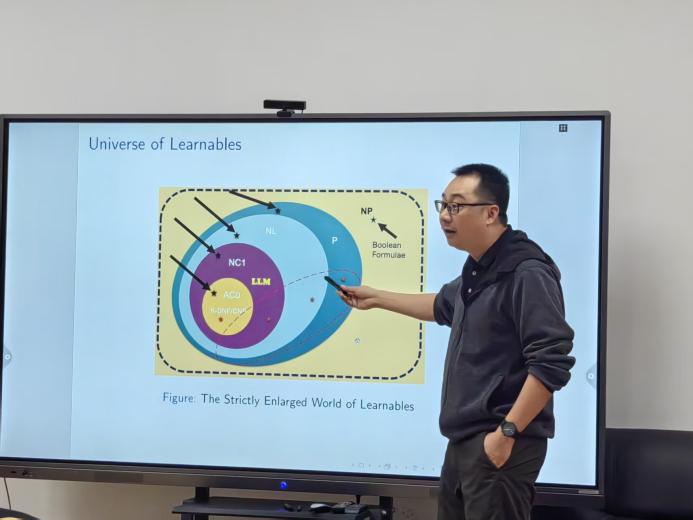
讲座最后，沈老师认为这一研究对计算学习理论具有积极的影响，围绕“计算机能学到什么？”这一问题做了丰富的讨论。他认为学习实际上是一种逼近，根据一些信息逼近得到一个布尔函数f。“学习”因此可以被定义为给定示例 1,f(x1)>,…, m,f(xm)>，算法构造函数f ʹ，使得f ʹ≈f（即f ʹ近似于f）。若存在一种算法能高效学习函数f，则问题f是可学习的。机器学习本质上是一种数据压缩，析取的信息与合取的信息非常容易压缩，而真正不可学习或难以学习的是那类不可压缩的真值表，即输入与输出极其无规律、无法用简单函数进行描述的类型。除非密码系统失效，否则NC¹类布尔公式不可学习，正如上文所说它包含伪随机函数（prf），受自然证明壁垒限制，学习难度极高。沈老师最后给出了逻辑程序计算问题与可学习问题之间关联关系的猜想。该猜想的解决意味着一些较难的可解问题依然可能是机器可学习的。

在点评互动环节，学院师生对人类思维及情感与机器学习是否类似、容量足够大的大模型能否将不可学习的内容转变为可学习的、动态逻辑是否有助于解决这类问题等内容展开热烈讨论，沈老师做了详细且精彩的解答。本次讲座历时两小时，现场听众互动积极，反响热烈。活动尾声，在全体与会者的热烈掌声中，讲座圆满结束。

供稿人：ok138cn太阳集团古天乐 张晓彤

初审丨吴朋飞

二审丨陈敬坤

终审丨尤   洋